〜応用編〜
解法テクニックの紹介
|
これからは、少し高度な解法テクニックを紹介していきます。 これを身につければ、Level Normalくらいはクリアできるようになるでしょう。 |
点のまわりの定理(2)
|
基礎編で説明した定理に加えて、
以下のようなことを知っておけばパズルを解く上で大きな助けとなるでしょう。
|
|
|
【定理2-1】 ある点の周りで1方向が「×」、1方向が「線」の場合は、残り2方向のうち一方が「×」、もう一方が「線」となる(二択)。 |
→
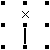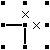or
|
|
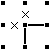
【定理2-2】 ある点の周り2方向が「×」の場合は、残り2方向が両方とも「×」または「線」となる(二択)。 |
→
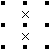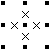or
|
|
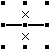
上の「二択」の法則を逆から考えてみると、さらに次のような法則もみちびけます。 こういう考えを実際に使うことはめったにない ( たいてい他の方法で解ける ) でしょうが、 何かの役に立つかもしれません。特にLevel Hardを解く時などは・・・ |
|
|
【定理2-3】 ある点の周りで1方向が「×」、 2方向のうちどちらか一方のみが「線」となることが分かっているとき、 残りの1方向は「線」となる。 |
→
|
|
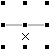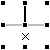
【定理2-4】 ある点の周りで1方向が「線」、 2方向のうちどちらか一方のみが「線」となることが分かっているとき、 残りの1方向は「×」となる。 |
→
|
閉ループの法則
|
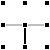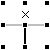
● 考えてみれば当たり前のことなのですが、2つ以上の輪に分かれてはいけないので、
右図のような場合、小さい輪 ( 閉ループ ) を作ってしまうような線をひくことはできません。
よって、「×」をつけることができます。 右のような小さい輪の場合は問題ないのですが、 かなり大きな輪でこういうパターンがよく出てきます。 そういう時に「×」をつけることを見逃さないようにしましょう ! |
→
|
共通部分確定法〜応用編〜
|
基礎編で説明したことに加えて、いくつかのポイントを押さえておけば、
この方法をさらにいろんな場合に応用することが出来ます。 まずは、上で説明した「点の周りの法則(2)」から考えられる、押さえておきたいポイントを説明します。 （横のラインを確定させようとしている場合を考えます。） |
|
| ● 上下一方のみに「線」の場合、 その点をまたいで線を引くことが出来ません。 |
→
|
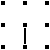| ● 上下のうち一方「線」で、もう一方が「×」の場合、 必ずその点が連続する線の端になります。 |
→
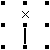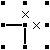or
|
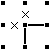
| ● 上下両方とも「×」の点がｎ個連続している場合、 「ｎ＋１」以上の長さの線が引かれる可能性がなければ、 それらの点の残りの方向はすべて「×」となります。 |
→
|
|
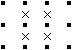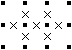
例を使って説明しましょう。下図パターンは、何もない場合はまったく決まりません。  ところが、このように確定している部分があった場合はどうでしょう。 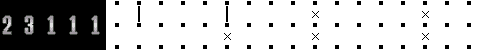 まず、左から2番目の点をまたいで線を引けないので、一番左から「2」の線が始まっている可能性が消えます。 では、次の「3」の線は一番左だとどこから始まるか・・・という風に考えていけば、一番左に寄せたパターンはこうなります。 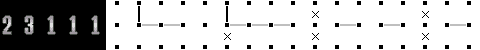 同じようにして、一番右に寄せたパターンはこうなるのです。 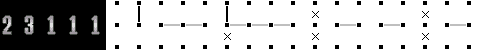 その共通部分をとると、こうなります。何もない場合は何も決まらなかったものが、 4ヵ所条件を増やすとこんなに確定してしまいます。 どうですか? まったく難しくないでしょう? これだけ出来ればLevel Normalは解けるはずです。  |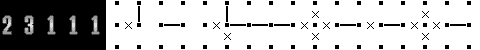
|
端から攻めろ !
|
問題を解いていく上での基本戦略は、とにかく端から順に確定させていくことです。
それは、線を伸ばせる方向が少ないため、決まりやすいのです。 右の例では、それぞれの行の左端は線がひかれることは点の周りの法則から考えても明らかですが、 それに加えて、その線は行の左端なので、数字の並びの左端「3」と「6」に対応していることがすぐに分かります。 ですから、その数だけ線を伸ばすことができます。 |
 ↓  |
| こういう考え方は、「仮定」を使う場合にも有効です。 Level Hardなどでは、理詰めだけで考えていては必ず行き詰まります。 そこで「仮定」を使ってみるのですが、どこを「仮定」するかということが問題になります。 そういう時は、「端から攻めろ ! 」の戦略を思い出し、 端の方で「これはないだろう」というような部分を仮定して見ることです。 そうすれば、光明が見出せるかもしれません。 | |
WebDS
もどる
|